The physics exam is bound to have quite a few derivations, which happen to be your best shot at scoring marks. You only need to write down pre-possessed knowledge and unlike a numerical, there are no complex calculations. With practice you can answer them very quickly and create time for other challenging questions.
The best way to remember a derivation is to understand the logic behind it and then practice, practice, practice. Your reference book will often provide a more comprehensive and understandable derivation than the NCERT textbook. If you are able to make a list of all the equations in the order that they appear in the derivation and link them logically, then you are on the right track. Flag any derivations that you don’t remember or can’t understand, make a sequential list of all the equations related to them and draw the relevant diagrams. Revise these lists as often as possible.
The presentation of a derivation matters as much as the derivation itself.Remember, this is a physics paper, not simply a list of mathematical equations.
Let’s say you want to derive the formula for the electric field generated by a uniformly charged, infinitely long straight wire using Gauss’ theorem.
Begin by drawing a relevant, well-labelled diagram. Don’t forget to use a scale.
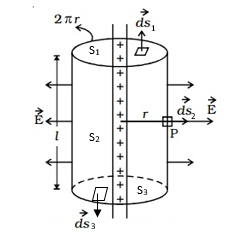
Describe the situation given to you and define any variables that you will be using.
Consider a uniformly charged, infinitely long straight wire. Let its linear charge density be λ and the electric field generated by it at any point be E. If q is the charge on length l of the wire, λ = q/l. We wish to find the electric field at a point at a distance r from it. The electric field due to the wire is radially outwards and uniform in magnitude at all points equidistant from the wire.
Describe the factors you will introduce in the derivation.
Consider a cylinder of radius r and height l, as shown with the diagram, with surfaces S1, S2 and S3. Let ds1, ds2 and ds3 be the small area element of the cylinder associated with each of these surfaces. Let φ1, φ2 and φ3 be the electric flux through each of these surfaces. E is perpendicular to ds1 and ds3 and parallel to ds2.
Any external equations you use must be explicitly mentioned. Justify all simplifications that you make.
We know, φ = E.ds
∴ φ1 = ∫dφ1 = ∫E.ds1= 0 [since E and ds1 are perpendicular]
φ3 = ∫dφ3= ∫E.ds3 = 0 [since E and ds3 are perpendicular]
φ3= ∫dφ 2= ∫E.ds2 = E∫ds2 [since E and ds2 are parallel]
= ES2 [since ∫ds2 = S2]
= E*2πrl
Number any equations you require later on in the derivation.
Total flux through the cylinder, φ = φ1 + φ2 + φ3
= E*2πrl …(i)
By Gauss’ theorem, flux through a closed surface, φ = q/εo …(ii)
By equations (i) and (ii),
E*2πrl = q/εo
E = q/ 2πrlεo
= λ/ 2πrεo [since λ = q/l]
By using the above technique you ensure that you obtain full marks in the derivation, and also impress the examiner – that makes a difference. Following the above suggested technique does not take much time.
Hope this helped! Good luck!
Comments